UNIVERSIDADE DE SÃO PAULO
FACULDADE DE FILOSOFIA, LETRAS E CIÊNCIAS HUMANAS
DEPARTAMENTO DE HISTÓRIA
JULIANA AKEMI RODRIGUES SO
“Sequência: A Geometria nos livros didáticos do Ensino Fundamental”
SÃO PAULO
2017
JULIANA AKEMI RODRIGUES SO
Sequência: A Geometria nos livros didáticos do Ensino Fundamental
Trabalho de sequência didática abordando o ensino da Geometria em alguns livros didáticos produzidos em diferentes tempos da disciplina FLH0423.
professora: Drª. Antonia Terra de Calazans Fernandes
SÃO PAULO
2017
SUMÁRIO
INTRODUÇÃO……………………………..…………………..……………………………..4
OBJETIVOS DE APRENDIZAGEM……………………………..………...……..……………………………..4
ABORDAGEM/METODOLOGIA ESCOLHIDA……………..…………………….………..4
JUSTIFICATIVA…………..………………..…………………..………………….…………..4
ATIVIDADES PROPOSTAS PARA A SEQUÊNCIA DIDÁTICA DENTRO DE UM CRONOGRAMA DE AULAS PREVISTO……...……………..……………………………..5
DOCUMENTOS UTILIZADOS………………………..……………………………..6
REFERÊNCIAS…………………..........……………....………..………..…………………..28
INTRODUÇÃO
É conhecido o problema com o entendimento da Matemática nas escolas, não só brasileiras como no mundo todo. Com o objetivo de entender um pouco mais sobre o processo do ensino da Geometria, campo pelo qual me interesso muito, durante alguns períodos da do século XX, esta sequência didática apresenta algumas fotos de tais livros para que então se faça uma reflexão sobre o processo de ensino.
OBJETIVOS DE APRENDIZAGEM
- Analisar documentos (fotos) criticamente
- Discutir ideias/percepções com a classe
- Propor algo novo para o ensino da Geometria no Brasil
ABORDAGEM/METODOLOGIA ESCOLHIDA
Para esta atividade foram escolhidos livros de 1932, 1987 e 1989. Escolhe-se fazer uma análise dos documentos e a partir desta propor uma discussão entre os alunos, colocando suas principais ideias em uma discussão maior com toda a sala e o professor. A partir deste momento é feita a análise do professor, retomando pontos que alunos já levantaram e introduzindo um entendimento sobre o conhecimento matemático que estaria presente nos livros didáticos. É evidente o teor crítico das colocações feitas para o professor, com o objetivo de questionar a classe.
JUSTIFICATIVA
Entende-se que é importante que não sejam apresentados contextos históricos/conteúdos matemáticos antes de serem feitas tais discussões justamente para que o aluno traga suas visões e conceitos já obtidos antes da aula para a discussão, de forma a fazer uma aula mais produtiva.
Livros de outros anos não entraram na seleção para esta sequência pois além de serem mais difíceis de serem achados, quando o são, geralmente são voltados para o Ensino Médio/Ginásio, Escolas Técnicas e Faculdades, o que foge do foco do trabalho presente que é o ensino da Geometria no Ensino Fundamental. O livro publicado no ano de 1989 “Matemática: educação e o desenvolvimento do senso crítico: 3ª série” se encontra na seleção por motivos comparativos, já que apresenta uma metodologia diferente sobre o ensino que pode ajudar os alunos a pensarem suas próprias abordagens.
ATIVIDADES PROPOSTAS PARA A SEQUÊNCIA DIDÁTICA DENTRO DE UM CRONOGRAMA DE AULAS PREVISTO
1. IDENTIFICAÇÃO
Público alvo: Formação de professores (na graduação e/ou professores já formados)
Disciplinas envolvidas: Matemática e História
Carga horária: 2 aulas de 2 horas para análise de documentos e discussão
Duração: 1 semana
Ano: 2017
2. MATERIAIS
- Notebook e retroprojetor (caso seja possível) para a visualização dos documentos
- Caso não seja possível (ou mesmo por escolha didática), utilizar documentos em forma impressa e distribuir em grupos
3. AULAS
- AULA 1
Nesta aula o professor deve introduzir o conteúdo que será abordado, no caso a Geometria no Ensino Fundamental no Brasil no século XX, de forma a ser claro e breve, tentando não influenciar as primeiras impressões dos alunos acerca do material.
São então mostrados os seguintes documentos dizendo suas datas de publicação (respectivamente de 1932, 1987 e 1989) e colocando seus nomes no slide (caso não seja utilizado retroprojetor, escrever o nome dos livros na lousa).
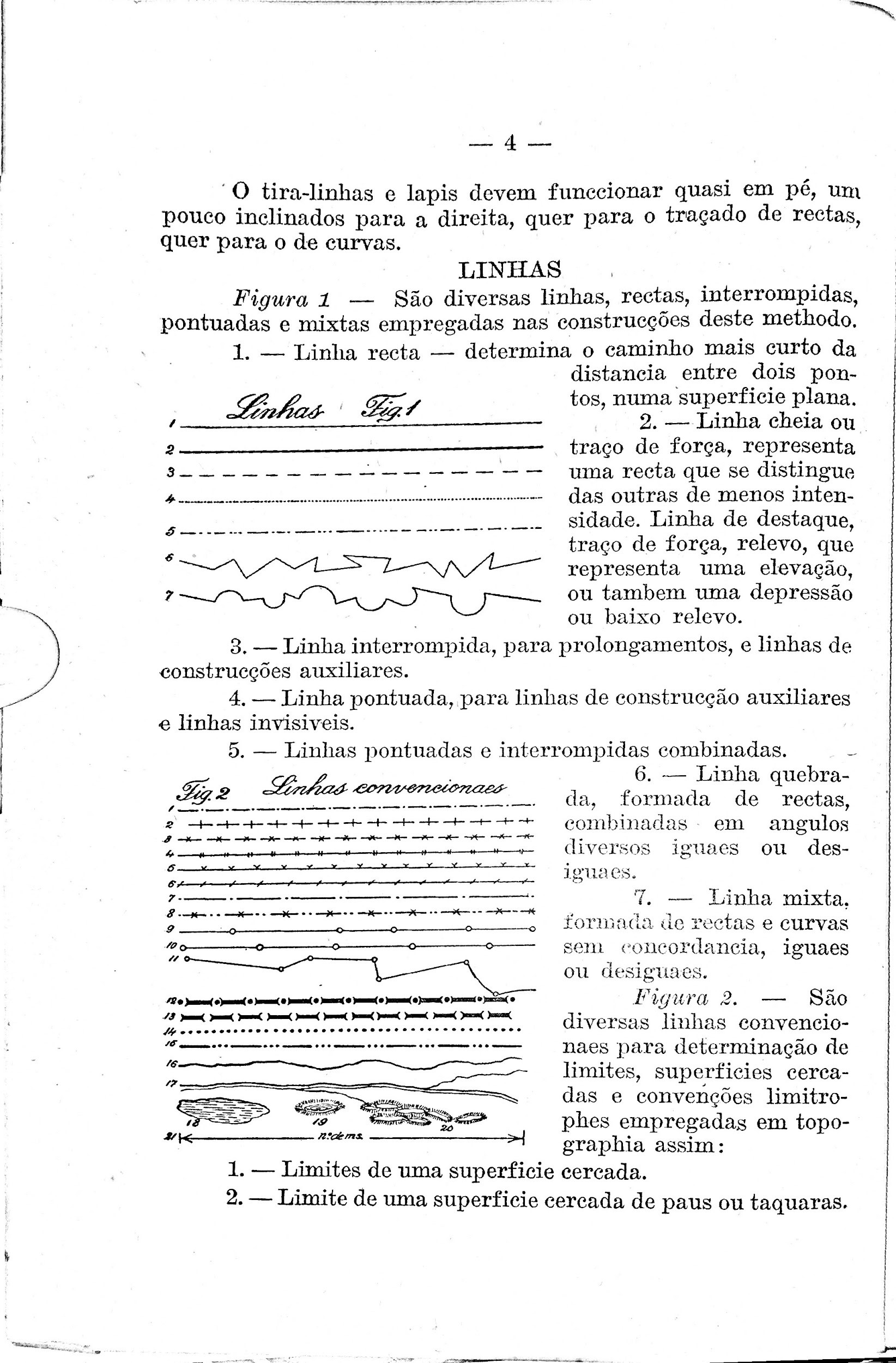
GALLINA JUNIOR, Luiz. Desenho linear geométrico. São Paulo, SP: Typ Siqueira, 1932, p. 1-5, 17, 21, 23.






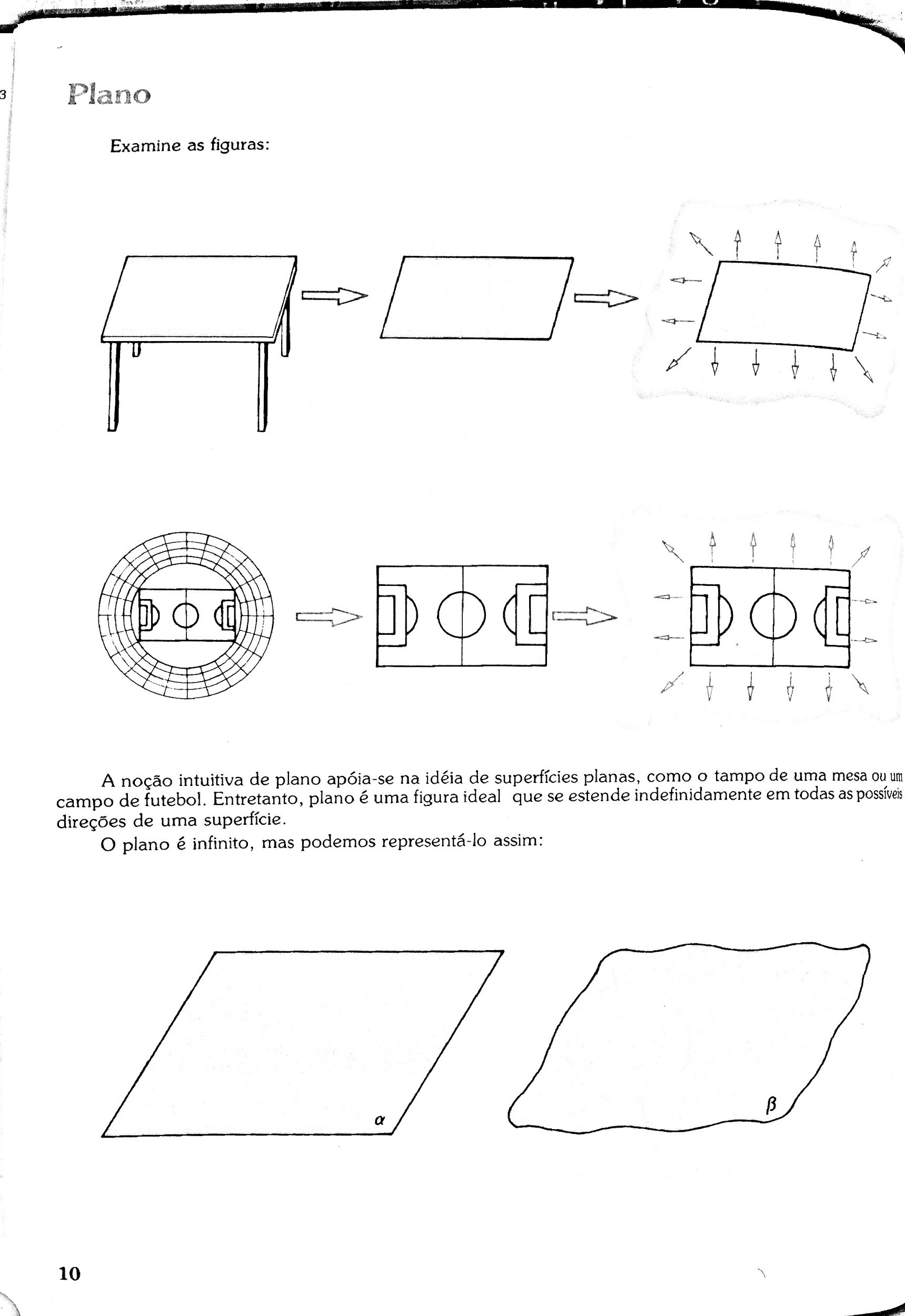
TEIXEIRA LOPES, Elizabeth; KANEGAE, Cecília Fujiko. Desenho geométrico: volume 1. São Paulo, SP: Scipione, 1987, p. 1, 7, 8, 10.



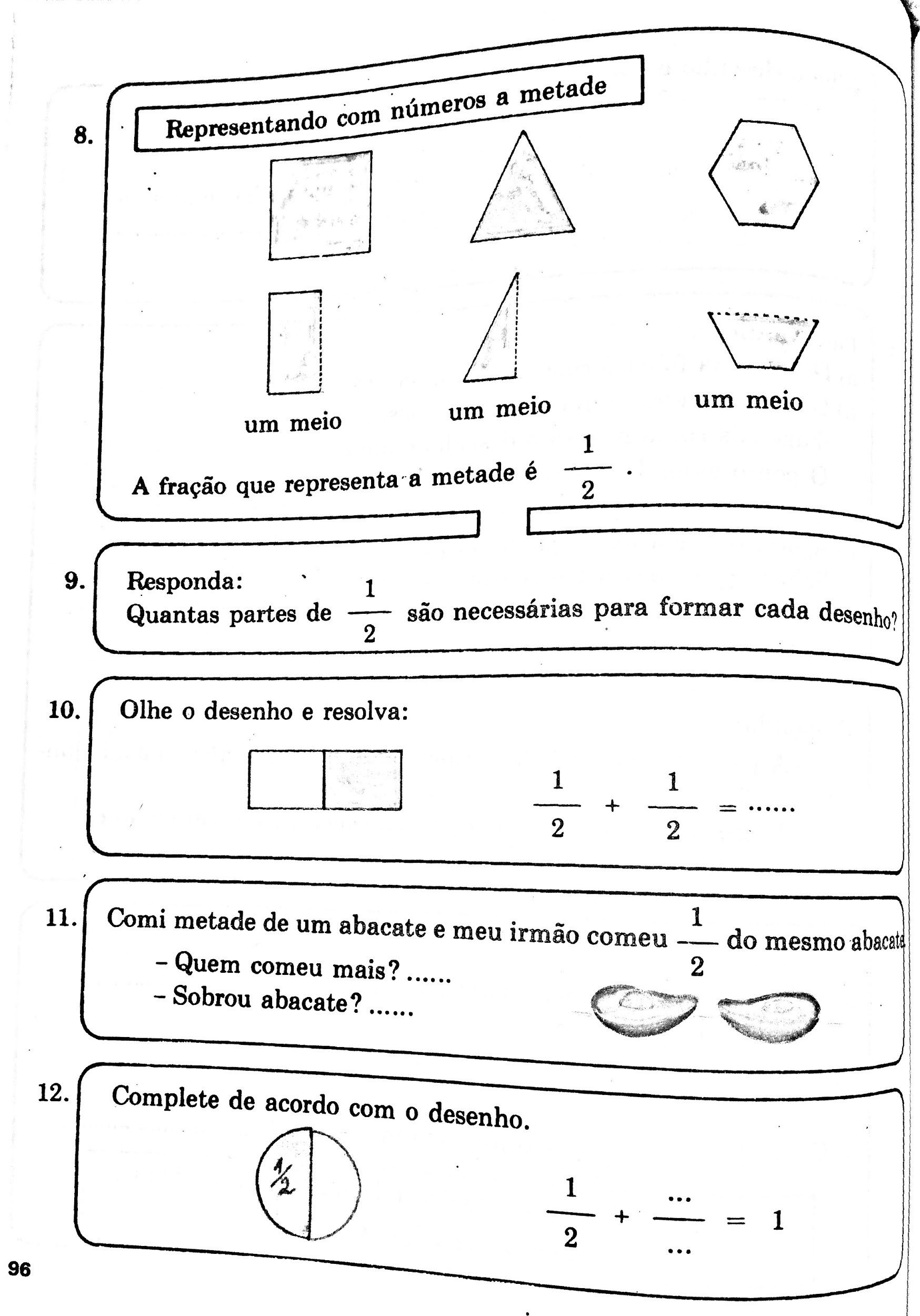
GARCIA, Tânia Maria Figueiredo Braga; SOARES, Maria Tereza Carneiro. Matemática: educação e o desenvolvimento do senso crítico: 3ª série. São Paulo, SP: Editora do Brasil, 1989, p. 1, 6, 7, 9, 15, 96, 132, contra-capa.







Em seguida é dado um tempo para que os alunos possam olhar os documentos com mais calma, discutir em grupos e formular o que trarão para a discussão com o professor e com o restante da sala.
Neste plano de aula são colocados pontos que são importantes de serem abordados pelo professor após os alunos terem levantado suas hipóteses/opiniões. Obviamente cabe ao professor discernir a escolha do que ele irá analisar para seus alunos, porém é interessante sempre ter um olhar mais crítico sobre o material. Tais pontos são somente um primeiro olhar motivador para os alunos, mais adiante serão colocadas outras colocações que acho interessante de serem feitas em um momento de análise mais profunda.
- No documento de 1932 e no de 1987 aparecem instruções de como manusear o material de desenho geométrico. Como são tais instruções? Diferem muito de época para época? Quais são suas (dos alunos da disciplina) opiniões sobre isso?
- No documento de 1932 não é utilizado o ente geométrico “reta”, e sim “linha”. Como a explicação deste conceito difere do conceito de “reta”? Isso influencia no entendimento do aluno sobre a matéria que vai estudar?
- Apontar que no documento de 1932 são colocados exemplos visuais (da “vida real”) dos conceitos.
- No doc. de 1932 também é explicado o material “transferidor”. De que forma é feita tal explicação? Vocês acham necessária tal colocação?
- Apontar o modo com que é feita a explicação da construção geométrica no documento de 1932.
- No documento de 1987 é colocado o conceito de “ponto” como ente geométrico. Porém não se explica o que é um ente geométrico. Seria necessária tal explicação? Se sim, de que modo?
- Mostrar que novamente aparecem exemplos do “mundo real” nos documentos de 1987 e 1989. No de 1987 para introduzir o conceito de “plano”.
- O documento de 1989 não apresenta instruções de manuseio de material, além de apresentar uma metodologia diferente de ensino. O que vocês puderam perceber?
- Mesmo que não seja tão pertinente (mas ainda sim pertinente, ora, temos a divisão de um círculo para a construção de um relógio!) para o ensino da Geometria, o documento de 1989 faz uma abordagem interessante, em minha opinião, acerca dos sistemas de numeração. Vocês conheceram outros sistemas de numeração na escola? Quais aspectos positivos/negativos vocês acham que tal assunto pode ter na percepção do aluno?
- No documento de 1989 existe uma parte para falar de linhas e pontos, mas tais conceitos geométricos também são abordados em outras partes. O que acham disso?
- Na contra-capa da do livro de 1989 se encontra uma imagem bastante conhecida. O que vocês conseguem dizer sobre ela? E sobre os conteúdos do livro?
- Vocês se lembram de como era o ensino da Geometria/Desenho Geométrico nos livros didáticos ou apostilas que tiveram quando estavam no Ensino Fundamental?
Após tais levantamentos do professor, a aula 1 se encerra de forma a deixar os alunos refletirem sobre tais materiais, para que na próxima aula se retomem alguns pontos e discutir sobre as perspectivas dos alunos sobre como deveriam ser ensinados tais conteúdos.
- AULA 2
Retomando o tema do curso e mostrando novamente os documentos dos livros didáticos, o professor retoma alguns pontos levantados na Aula 1 para que possa colocar outros pontos, a fim de uma análise mais crítica.
- Lembrar os alunos que todos os conteúdos ensinados para o Ensino Básico partem de Parâmetros Curriculares Nacionais, os quais são elaborados partindo de exames internacionais. Portanto a elaboração de um currículo está intrinsecamente ligada à políticas internacionais, não bastando de uma simples escolha do professor de ensinar ou não algum conteúdo.
- Partindo disso, qual o papel do professor? Na perspectiva do curso seria alguém que pudesse articular com sua classe (de professores) e repensar tal currículo mas também se reinventar em sala de aula para que tais conteúdos sejam aprendidos com qualidade.
- Pensando no conteúdo:
- Para o Ensino Fundamental qual seria o nível de complexidade ideal para ser incluído nas explicações? ex: explicação do documento de 1932 sobre o conceito de “linha”
- Sob a perspectiva de Van Hiele, existem níveis de aprendizagem que devem ser seguidos no ensino da Geometria, pois o aluno não conseguirá entender n se não conseguiu entender n-1. Assim, o casal Van Hiele traz cinco níveis de entendimento, que devem ser seguidos a cada novo conceito:
- Nível 1: Visualização ou reconhecimento.
- Nível 2: Análise.
- Nível 3: Dedução informal ou classificação.
- Nível 4: Dedução formal.
- Nível 5: Rigor.
Nessa perspectiva, como os alunos da disciplina entendem que isso ocorre nos livros apresentados?
-
- Compreendendo que é necessário um cuidado nas construções geométricas mas também entendendo que o ensino deve ser divertido e intuitivo, quais as opiniões dos alunos sobre as instruções nos documentos de 1932 e 1987 e a falta destas no documento de 1989?
- O documento de 1989 está estruturado de forma diferente dos outros. Em seu nome aparece a ideia de “crítica”. Os alunos vêem tal desenvolvimento de crítica a partir da estruturação? Mais importante, acham importante desenvolver a crítica? (Deixar claro que a perspectiva do curso é justamente essa)
- Como curiosidade, mencionar que na ditadura militar argentina em 1978, a geometria analítica (de uso de vetores) foi condenada pois o conceito de “vetor” apresentaria, de forma sutil, uma ideologia revolucionária marxista.¹
- Apontar que houveram momentos em que foram introduzidas explicações sobre materiais, mas no documento de 1989 não houve. Colocar nomes ou não? Cobrar os alunos (do Ensino Fundamental) para decorarem tais nomes e explicações ou não?
Neste momento o professor deve colocar os alunos novamente em grupos (livre formação) para que discutam suas propostas de como deveria ser o ensino da Geometria no Ensino Fundamental e, principalmente, como articular as aulas com o livro didático (caso use livro didático). Um dos integrantes de cada grupo deverá escrever as propostas conjuntas do grupo em um papel e entregar para o professor, como forma de avaliação da disciplina (não de “certo” e “errado”, mas sim se conseguiram compreender os embates que existem no ensino da Geometria).
REFERÊNCIAS
GALLINA JUNIOR, Luiz. Desenho linear geométrico. São Paulo, SP: Typ Siqueira, 1932, p. 1-5, 17, 21, 23.
TEIXEIRA LOPES, Elizabeth; KANEGAE, Cecília Fujiko. Desenho geométrico: volume 1. São Paulo, SP: Scipione, 1987, p. 1, 7, 8, 10.
GARCIA, Tânia Maria Figueiredo Braga; SOARES, Maria Tereza Carneiro. Matemática: educação e o desenvolvimento do senso crítico: 3ª série. São Paulo, SP: Editora do Brasil, 1989, p. 1, 6, 7, 9, 15, 96, 132, contra-capa.
- Boletim da Adunicamp, encontrado no site: https://www.ime.usp.br/~ivanstru/Site/MAT105-2017_files/BoletimAdunicam…

